BODMAS: My Complete Guide to the Order of Operations

What is the BODMAS rule in Australia? What is the importance of BODMAS?

BODMAS is a standard order of operations in mathematics used to avoid ambiguity and ensure a single correct answer for any given expression. A simple example of 1+2×3 can give different answers such as 1+2×3 = (1+2)×3 = 3×3 = 9 or we can have 1+2×3 = 1+(2×3) = 1+6 = 7. Hence, to ensure that everyone gets the same answer, BODMAS rule is used.

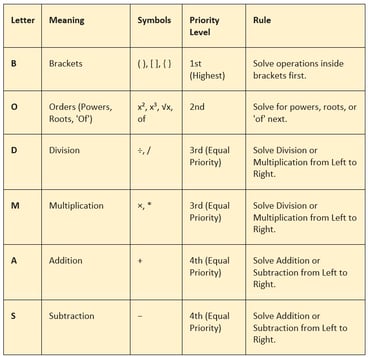
As per BODMAS rules calculations in brackets must be made first, followed by calculations involving indices (powers, exponents), then multiplication and division (Working from left to right), and finally, addition and subtraction (Working from left to right)

BODMAS is used in the UK and Commonwealth countries such as Australia whereas some other countries such as USA may use PEMDAS ((Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) to define the correct sequence for performing mathematical operations. However, both operations are the same and will lead to the same answer.

How do you do BODMAS step by step?

The BODMAS Rule: Step-by-Step Calculation Guide to be solved in the following order:

1. Brackets: Solve all operations inside brackets first, starting with the innermost set if they are nested.

2. Orders: Next, evaluate any powers, roots, or 'of' operations.

3. Division and Multiplication: Then, perform all division and multiplication operations. Remember, these have equal priority, so work through them from left to right as they appear in the expression.

4. Addition and Subtraction: Finally, perform all addition and subtraction operations. These also have equal priority and must be worked through from left to right as they appear.

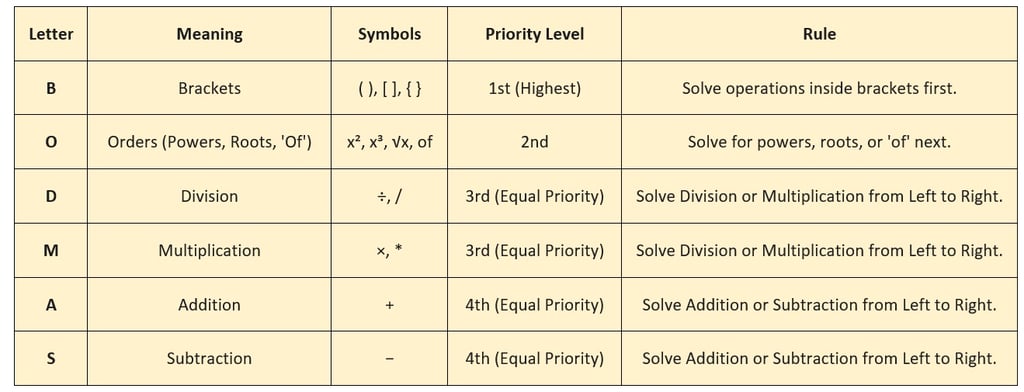
BODMAS step by step summary is shown in the following table:

Example: Consider the expression 9 ÷ 3 × 3.

• First, perform the division (leftmost operation): 9 ÷ 3 = 3.

• The expression becomes 3 × 3.

• Then, perform the multiplication: 3 × 3 = 9. Hence, The correct answer is 9.

Example: Consider the expression 8 × 2 + 3.

• First, perform the multiplication (leftmost operation): 8 × 2 = 16.

• The expression becomes 16 + 3.

• Then, perform the addition: 16 + 3 = 19. Hence, The correct answer is 19.

Example: Consider the expression 8 × (2 + 3).

• First, perform the addition (Inside the bracket): 2 + 3 = 5.

• The expression becomes 8 × 5.

• Then, perform the addition: 8 × 5 = 40. Hence, The correct answer is 40.

Example: Consider the expression: 4² × 24 ÷ (9 + 3) + 4 - 5

Step 1: Brackets first
9 + 3 = 12
Expression becomes:
4² × 24 ÷ 12 + 4 - 5

Step 2: Indices (Orders)
4² = 16
Expression becomes:
16 × 24 ÷ 12 + 4 - 5

Step 3: Multiplication and Division (from left to right)
First: 16 × 24 = 384
Then: 384 ÷ 12 = 32
Expression becomes:
32 + 4 - 5

Step 4: Addition and Subtraction (from left to right)
32 + 4 = 36
36 - 5 = 31

Sample BODMAS Examples with step by step answers?

Why Following BODMAS is Important?

Adhering strictly to the BODMAS rule is fundamental in mathematics for several key reasons:

Getting the Right Answer (Accuracy): The primary reason for BODMAS is to ensure accuracy. Following the correct order of operations is the only way to guarantee the correct result for expressions involving multiple operations.4 Deviating from the sequence, such as simply working from left to right without considering operation priority, will frequently lead to incorrect answers.2

Everyone Understands (Consistency & Clarity): BODMAS provides a standard, universally accepted convention for interpreting mathematical expressions.4 It acts like a common language, ensuring that any mathematical statement is read and solved the same way by everyone, regardless of their background or location.3 This eliminates ambiguity and makes mathematical communication clear and precise.2 This shared understanding is crucial, especially as calculations become more complex in fields like science, engineering, and finance.2 The convention allows mathematical notation to remain brief while being unambiguous.

Building Blocks for Future Math: Mastering the order of operations through BODMAS is not just about solving current arithmetic problems; it's a foundational skill essential for success in more advanced mathematics.4 Concepts in algebra, calculus, and beyond rely heavily on correctly manipulating complex expressions. A solid understanding of BODMAS provides the necessary groundwork for tackling these future challenges confidently.

Quick Recap & Practice Tips

Remembering and applying BODMAS correctly takes practice. Here’s a quick summary and some helpful tips:

BODMAS Checklist: When solving an expression, follow these steps in order:

1. Brackets (Solve inside first, innermost outwards)

2. Orders (Powers, roots, 'of')

3. Division and Multiplication (Work from left to right)

4. Addition and Subtraction (Work from left to right)

Practice Power: The best way to master BODMAS is through regular practice. Work through various problems involving different combinations of operations.2 The more problems solved using the rule, the more intuitive it becomes.

Use Brackets to Clarify: If an expression seems confusing, adding extra parentheses (that follow the BODMAS rules) can sometimes help break it down into smaller, more manageable steps.2

Double-Check: After finding an answer, take a moment to review each step of the calculation. Ensure that the BODMAS order was followed correctly at every stage to catch any potential mistakes.4

By understanding and consistently applying the BODMAS rule, students can build confidence in their mathematical abilities and ensure accuracy in their calculations.